AC自动机多模式匹配
Aho–Corasick算法是由Alfred V. Aho和Margaret J.Corasick 发明的字符串搜索算法,用于在输入的一串字符串中匹配有限组“字典”中的子串。它与普通字符串匹配的不同点在于同时与所有字典串进行匹配。
算法理解
AC算法核心在于将所有需要匹配的字典模式构造了一个自动机,自动机的每个状态代表了经历一定的输入字符串后到达的状态节点,这个状态节点可能对应一组输出,这组输出就是从之前一个状态到当前状态新匹配到了哪些字典模式。根据输入从一个节点跳转到另一个节点。
单纯的字典查找可以用Trie树解决,但是Trie树只能精确匹配输入是否符合某个字典模式。对于输入中是否存在某些子串匹配了字典中的某些模式Trie树无法支持。原因可以从两方面看。一是Trie树遍历输入字符串遇到无法匹配的字符时无法继续运行。二是Trie树节点只记录了当前节点是否匹配了某个字典模式,但多模匹配还可能出现输入字符串到达某个节点时,输入的后缀匹配了某个字典模式,这也就是输入字符串的中间子串匹配了某些模式。
AC自动机可以看作是以Trie树为基础结构,进一步扩展完成了上面的两个要求,从而对输入字符串可以进行多模式的高效子串匹配。
模式匹配算法高效运行的一个要求是要尽可能高效的利用输入字符串已经扫描过的部分。从KMP算法可以看到当出现字符匹配失败时,这种高效利用就需要在当前输入中尽量保留有价值的部分,在子串匹配中这种价值就是当前输入的后缀可以匹配到某个模式的前缀,当有多个后缀都可能匹配时,最长的那个后缀就是最有价值的,因为包含了其他的较短后缀。AC算法对于字符匹配失败时的处理方式也是这种思路。
算法构造
以模式集合{he,she,his,hers}为例,记录AC自动机的构造过程。算法中涉及到三种表,分别是goto表、failure表、output表,在下面描述AC自动机构造时会介绍。
goto表
AC自动机构造第一就是用所有的字典模式构造一个Trie树,在算法中也称为goto表,在每个字符输入后根据goto表中的记录完成下一个状态节点的跳转。
初始状态0,添加”he”后新增了两个状态,分别是状态0接收输入字符’h’跳转到状态1,状态1接收输入字符’e’跳转到状态2。状态2加粗,这里表示该状态匹配到了相应的模式,也就是存在输出”he”,这个输出将是output表的一部分。

继续添加模式”she”,从状态0开始添加,同上一步一样,新增了状态3、4、5,状态5存在输出。
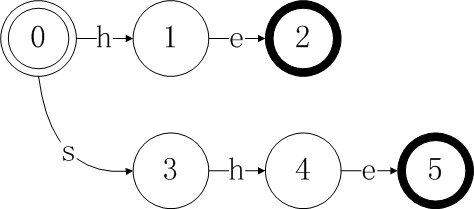
继续添加模式”his”,这里需要注意的是在一个状态遇到相同字符时要重复利用之前生成的状态和状态跳转,比如状态0接收字符’h’跳转到状态1是已经存在的。
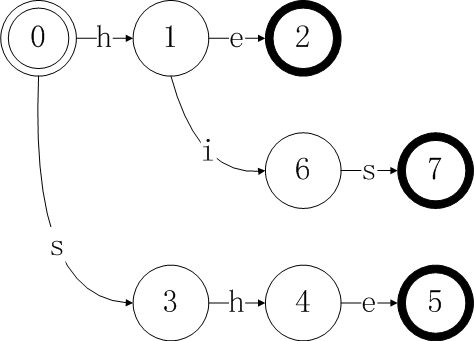
最后添加模式”hers”,到这里goto表构造完成。这里有一点特殊的是,字典添加完成后,状态0对于所有不合法的输入字符均跳转到其本身,也就是状态0合法接收所有输入字符。
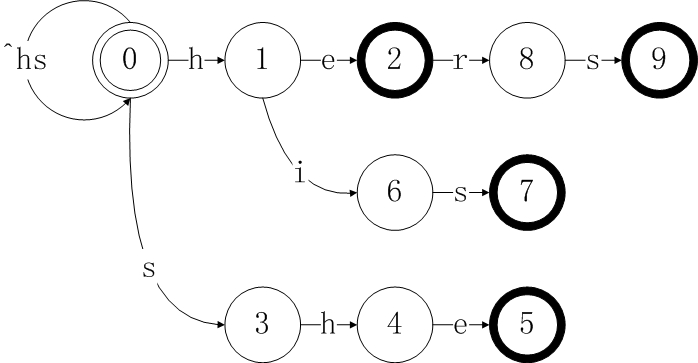
failure表
构造failure表前,先引入一个深度的概念,一个状态的深度是在goto表中从状态0到该状态的路径长度,这个路径是唯一的。
failure表的作用是在查找匹配模式时,处理匹配失败时的状态跳转。这种匹配失败时的状态跳转需要达成一个目标,就是跳转到的新状态节点代表了之前状态节点的输入字符串的一个后缀,因为这个新状态节点是在goto表中的,所以这个新状态节点必然也代表了某个模式的前缀,这种符合输入后缀匹配模式前缀的新状态节点可能有不只一个,那么failure表中只需要记录最长后缀的那一个跳转就够了,因为如果继续匹配失败会从failure表往更短的后缀跳转的。状态A的failure跳转是状态B,说明B代表了A的某一个输入后缀,因此如果状态B有输出那么就有必要将状态B的输出也整合到状态A的output表中。在failure跳转中一定是由深度大的状态往深度小的状态跳转。
- failure表的构造采用递归的思想。状态0是根节点,failure跳转为其自身。深度为1的状态节点failure跳转均为根节点。
- 假设深度小于d的所有状态,失效函数f都已经计算出结果。
- 那么对于深度为d的状态s。
- 假设其父节点为状态r,则存在字符a,满足g(r, a) = s,其中g为状态转移函数,代表了goto表。
- 修改r,使r = f(r),如果g(r, a)有意义,那么g(r, a)就是s的失效跳转节点。因为s的父节点与s仅差一个输入a,父节点的失效跳转节点是父节点的最长有意义后缀,如果继续输入a依然有意义,那么到达的节点将是s的最长有意义后缀。
- 如果g(r, a)无意义,那么继续使r = f(r),直到g(r, a)有意义。
- 如果r退回根节点,由于根节点对于一切输入均有合法跳转,因此s的失效跳转一定可以确定。
实际开发中,可以采用广度优先遍历goto表,逐层构造failure表中每个状态节点的失效跳转。
一个例子,状态4的failure状态。其父节点状态3的深度是1,失效跳转为根节点,根节点对于输入h有意义,状态转移到状态1,因此状态4的failure跳转就是状态1。可以看到状态4代表的输入字符串”sh”最长有意义后缀”h”的确是状态1所代表的输入。
根据上述逻辑,得到failure表。
| 状态 | failure |
|---|---|
| 1 | 0 |
| 2 | 0 |
| 3 | 0 |
| 4 | 1 |
| 5 | 2 |
| 6 | 0 |
| 7 | 3 |
| 8 | 0 |
| 9 | 3 |
将failure表用虚线表示,整合goto表。
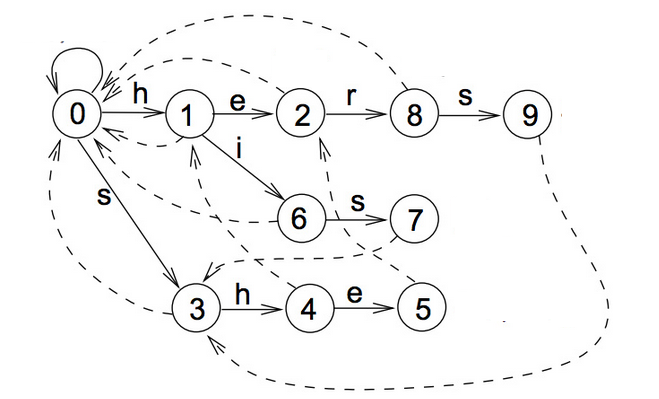
output表
output表,即到达某个状态节点时记录哪些模式匹配成功。构造过程分两步,在上面构造goto表和failure表时有提到。
- 构造goto表时,每个模式串结束的状态都加入到output表。
| 状态 | output |
|---|---|
| 2 | {he} |
| 5 | {she} |
| 7 | {his} |
| 9 | {hers} |
- 构造failure表时,由深度小的状态到深度大的状态,逐层构造failure表,同时每个状态节点的输出会合并其failure节点的输出,共同构成output表中该状态节点的输出。
| 状态 | output |
|---|---|
| 2 | {he} |
| 5 | {she, he} |
| 7 | {his} |
| 9 | {hers} |
PS: 这个例子中的合并了failure节点输出的状态节点,都是原本就有输出的状态节点,这是字典字符串集合选择的原因。实际情况中,会有原本没有输出的节点,在合并其failure节点输出过程中新增了输出。比如这个字典中如果增加字符串”i”,那么f(6)将会是新增的状态节点10,output(6)也会包含”i”。
查找匹配模式
- 从状态0开始逐个字符遍历输入的字符串,假设字符为a,如果goto表中当前状态对于字符a有合法跳转,则转移状态。对于转移到的状态节点检查output表的输出。
- 如果goto表中当前状态对于字符a没有合法跳转,则根据failure表转移状态,对于转移到的状态节点继续检查字符a,重复此过程直到对于字符a有合法跳转。由于根节点对于所有输入均有合法跳转,因此这个过程一定可以终结。
当输入字符可能的集合比较小时,比如一个字节8位有256种可能,可以在构造阶段对于每一个状态节点的所有输入合并failure表,构成一个确定的状态转移表,这可以避免一个输入字符多次failure时的多次查找操作,只需要一次状态转移就可以了。



